Social networks
By Erin Ochoa
Introduction
From microblogging with Twitter to leaving comments on YouTube videos, the use of online social media platforms has become a part of everyday life for many: as of January 2020, Kemp (2020) estimates that there are 3.8 billion active social media users—49% of the global population. With the inception of social media—the precursors of which arguably date to the 1970s, if not earlier—and its proliferation since the turn of the millennium, interest has grown around the theory and methods for analyzing data from such networking platforms. This type of research is a form of social network analysis.
Social networks among humans, however, have existed as long as humanity itself. This is because a social network exists whenever two or more social entities interact or otherwise relate to each another. Many such interactions and relations in contemporary society are fleeting: transactions between workers and customers in retail or service settings, strangers riding a train together, or students in the same class whose acquaintanceship ends along with the school year. Others may be formal, structured, deliberate, or otherwise durable: members of a given Senate committee serving in a given term of Congress, a hierarchy of workers in a company division, a marriage relationship between spouses, or kinship ties. It is these formal, structured, deliberate, and durable networks that are the primary focus of social network analysis.
What is a Social Network? What is Social Network Analysis?
A social network is a set of relationships among social entities. Social network analysis, then, is a body of methods used to evaluate the characteristics of social networks and their elements. To better understand what these terms mean, it is important to first address what a network is and what elements it comprises. We will also consider examples of networks and approaches to representing them.
Elements of a Network
A network is a set of entities and the relationships among them. The study of networks is rooted in a sub-field of mathematics called graph theory. From this perspective, a network is a data structure modeling a collection of units, which are represented as points called nodes or vertices, and the relationships among them, which are represented by links, called edges or ties, between the nodes. Two nodes that are connected by an edge are said to be neighbors. A network is also called a graph; here, both terms are used interchangeably.
Networks can represent many different types of real-world phenomena. Consider how a network could be used to model each of the following:
The genealogical history of the Japanese royal family:
- Nodes represent people; ties represent marriages and births.
Email correspondence between workers in a corporation:
- Nodes represent workers; ties represent emails exchanged between pairs of workers.
Flights between all the international airports in the world:
- Nodes represent airports; ties represent flights connecting airports.
Predator–prey relationships among animals in an ecosystem:
- Nodes represent different species; ties represent which animals prey upon others.
Mentorship and advising among political scientists in academia:
- Nodes represent scholars; ties represent mentor–student relationships among scholars.
The order in which blocks of code in a computer program could be executed:
- Nodes represent blocks of code; ties represent flow control between blocks.
Advice-seeking relationships among all current federal circuit judges in the United States:
- Nodes represent judges; ties represent whether a given judge has ever asked another judge for advice.
When the nodes in a network represent people, organizations, or another type of social entity, the graph can be called a social network.
Network Representations
There are different ways to represent a network. The two most accessible methods are sociograms and adjacency matrices. The sociogram in figure 10.1 and the adjacency matrix in Table 11.1 are representations of the same network.
![A sociogram for a network with nodes [A, B, C, D, E]. Each circle represents a node and each line represents a relationship between the two nodes it connects](images/social-networks/11-1.png)
| \(A\) | \(B\) | \(C\) | \(D\) | \(E\) | |
|---|---|---|---|---|---|
| \(A\) | — | \(1\) | \(1\) | \(0\) | \(1\) |
| \(B\) | \(1\) | — | \(0\) | \(1\) | \(0\) |
| \(C\) | \(1\) | \(0\) | — | \(1\) | \(1\) |
| \(D\) | \(0\) | \(1\) | \(1\) | — | \(0\) |
| \(E\) | \(1\) | \(0\) | \(1\) | \(0\) | — |
A sociogram is a diagram that displays the nodes as points and the edges as lines or arrows.
To understand how an adjacency matrix works, first recall that a matrix is a rectangular data structure containing numeric values which are organized in rows and columns; the total number of cells or values in the matrix equals the number of rows multiplied by the number of columns. An adjacency matrix is a square matrix that represents the presence or absence of ties between pairs of nodes in a graph—it tells us which nodes are adjacent, that is, which nodes are neighbors. There exists one row and one column for each node, and each cell value identifies whether the nodes associated with that cell are adjacent.
Method: Set-up/Overview
Two Fundamental Network Attributes
The two most fundamental attributes of a network are whether it is directed and whether it is weighted.
Note the arrows in the sociogram to the right; these indicate the direction of perceived friendship from one node to another. For example: the two-way arrow between Mega and Nyasha indicates that each considers the other a friend; the one-way arrow pointing from Kiko to Jaylen, however, indicates that Kiko considers Jaylen a friend, but also that Jaylen does not consider Kiko a friend –their relationship is asymmetric.
Undirected and Directed Networks
The first important attribute of a network is whether there is a direction associated with the modeled relationships between nodes. There are two types of graphs with respect to direction, undirected and directed.
Undirected Networks. The most basic type is an undirected graph, in which the edges represent symmetric, or reciprocal, relationships between nodes. The ties in an undirected graph are called undirected or symmetric ties. Such ties indicate that for any pair of connected nodes, both nodes have the same role in the relationship.
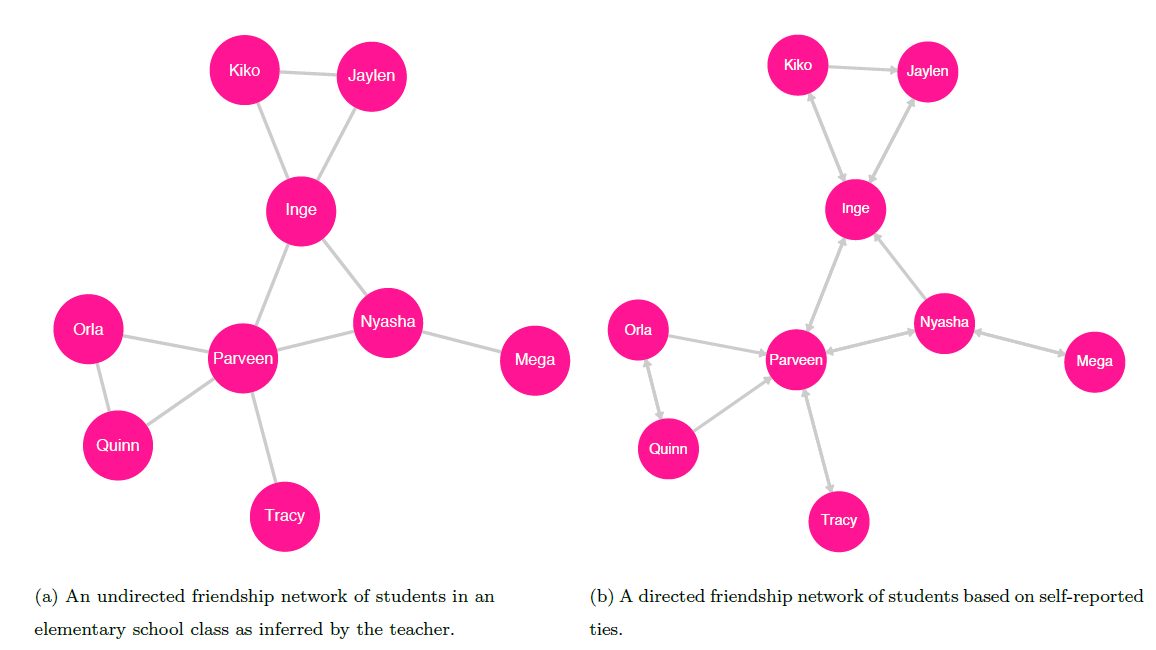
One example of such a graph is the friendship network of students in an elementary school class based on bonds observed by their teacher (see figure 10.2. In this network, an edge between two students means that their teacher perceives them to have a mutual friendship; note that a tie does not indicate any hierarchy among the connected nodes. If, for example, the teacher infers that Inge and Jaylen are friends, then an undirected tie exists between them in the graph. The edge between these two nodes means that to say Inge is friends with Jaylen is the same as saying Jaylen is friends with Inge.
Directed Networks. In a directed graph, each tie has a direction: the directed ties in a directed graph represent a one-way or asymmetric relationship between nodes. We can think of asymmetric relationships as those in which the roles of the source and destination nodes differ.
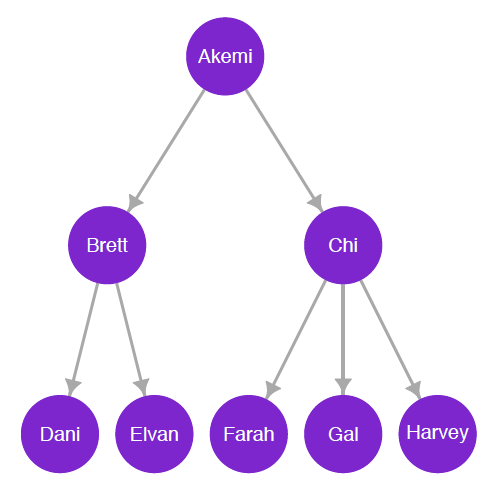
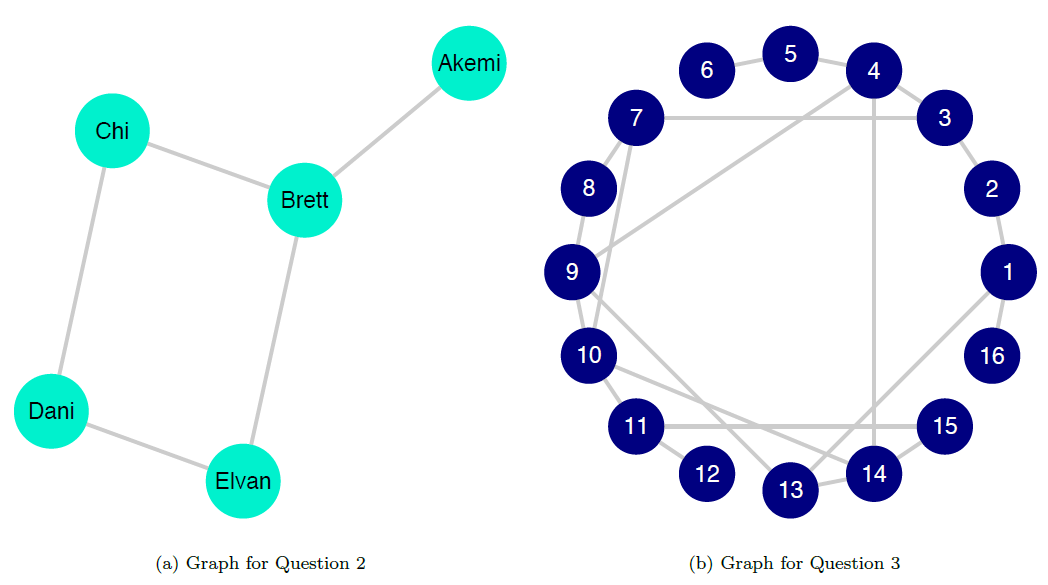
Earlier, we described a network to model mentorship and advising between political scientists (see figure 10.3). For each tie in this network, one node has the role of mentor and the other the role of student; note that each node can take on one role or the other, or even both depending on the direction of its ties to other nodes. Let there be eight scholars in the network: Akemi, Brett, Chi, Dani, Elvan, Farah, Gal, and Harvey. Akemi is the most senior scholar and was an adviser to Brett and Chi when they were graduate students. Later in their careers, Brett mentored Dani and Elvan, and Chi mentored Farah, Gal, and Harvey. In this network, the direction of the tie is a fundamental aspect of the relationship between two nodes: to say Akemi mentors Brett is not the same as saying Brett mentors Akemi.
A second example of a directed graph is the network of students in an elementary school class based on friendship ties identified by the students themselves 11.2: if Inge identifies Jaylen as a friend, then there exists a friendship tie from Inge to Jaylen; if Jaylen identifies Inge as a friend, then there exists a friendship tie from Jaylen to Inge. Kiko identifies both Inge and Jaylen as friends, so there exist ties from Kiko to Inge and from Kiko to Jaylen. Inge identifies Kiko as a friend, but Jaylen does not; thus, there exists a tie from Inge to Kiko, but there is no tie from Jaylen to Kiko—despite the tie from Kiko to Jaylen. The ability to denote such asymmetric relationships is the key feature of directed graphs.
Weighting
The second fundamental attribute of a graph is whether its ties are weighted. There are two types of graphs with respect to weighting, unweighted and weighted.
Unweighted Networks. In an unweighted graph, there are no values associated with any of the edges. The relationships represented in the network are modeled as equivalent, regardless of the circumstances surrounding each relationship.
Consider the earlier example describing a friendship network among elementary school classmates as observed by their teacher. In this undirected network, we can consider ties as dichotomous or binary: between two nodes, a tie either exists or not. Imagine that Inge and Jaylen have been neighbors, friends, and classmates for five years, and both are now friends with Loren, a new classmate who has recently moved to the neighborhood. In an unweighted representation of the friendship network, the tie between Inge and Jaylen is seen as equivalent to the tie between Inge and Loren: the network does not capture the strength, duration, frequency of contact, or other qualities of the friendship bonds, only whether the friendship bonds exist.
Weighted Networks. In a weighted graph, each edge has a numeric value or weight representing an attribute of the relationship between its two nodes. Depending on the network, the value can measure the physical distance between two nodes or some aspect of the strength or intensity of the relationship between them or perhaps of the frequency of an event that occurs between the two nodes.
A simple example of a weighted network is an undirected graph of several towns and the highways existing between them. In this network, the weight of each edge is the length of the highway connecting a pair of towns and thus measures the distance between them.
For a directed weighted graph, recall the earlier example of the email correspondence network among workers in a corporation. Consider the case of two workers, Stéphane and Tracy, each of whom has sent emails to the other. To make a directed weighted correspondence graph, assign to each edge the number of emails sent by the source node to the destination node: Stéphane has sent Tracy \(11\) emails, so the weight of the tie from Stéphane to Tracy is \(11\); Tracy has sent Stéphane \(15\) emails, so the weight of the tie from Tracy to Stéphane is \(15\). In this case, the edges represent the frequency and direction of email contact between the two workers.
It is possible to convert a weighted directed graph to a weighted undirected graph. This can be accomplished by summing the weights of ties between a pair of nodes and assigning the result to a single undirected edge between the nodes. For the email correspondence network, to replace the directed ties between Stéphane and Tracy with an undirected tie, we add Stéphane’s \(11\) sent emails to Tracy’s \(15\) and assign the value \(26\) to the link between them. The edges now represent the frequency, but not the direction, of email contact between Stéphane and Tracy.
A Note on Node Attributes. Real-world social entities vary in their characteristics—that is, there are variables associated with social entities. For example, there exist many types of organizations, such as non-profits, for-profit corporations, government agencies, and intergovernmental bodies. Similarly, there are a plethora of aspects associated with individual people. For example, consider the following: In the United States, generally speaking, age cutoffs define the legal categories of child and adult; persons with high-school degrees belong to one category, while those who have not attained a high-school education belong to a different one; and those with certain criminal convictions are labeled as felons.
In general, each variable associated with a social actor measures a single aspect of that actor: it may measure height or weight, but not both, for example. These variables may be quantitative (a number, such as the count of armed conflicts that have taken place in a district, or the fuel efficiency of a vehicle in miles per gallon) or qualitative (a category, such as a nation’s form of government, or whether a state’s legal code allows for capital punishment). (For a thorough discussion of variable types, see chapter on Data.
We can represent the different values of a variable across the vertices in a network using node attributes. Here, we will only consider node attributes that represent categorical variables, either nominal or ordinal. A variable may take on a single value from a finite set of all possible categories (the categories are exhaustive), with each category being distinct from all the others (the categories are mutually exclusive). Note, however, that discrete and continuous variables can be converted to ordinal variables by subsetting the possible values into categories. Consider, for example, a variable that captures the count of shootings in a neighborhood with categories such as 0-9, 10-19, 20-29, and \(\ge30\); or the weight status associated with each range of BMI values as classified by the CDC ((Centers for Disease Control and Prevention 2017)): \(\le18.5\) is classified as underweight, 18.5-24.9 as normal or healthy weight, 25-29.9 as overweight, and \(\ge30\) as obese.
In reality, social actors are associated with myriad characteristics, conditions, and states of being. A given scientific study may measure many such characteristics, with each constituting a single variable. While each variable can only take on a single value for a given observation, a node in a network may be associated with zero, one, or several variables. In the earlier example of a friendship network among elementary-school students as inferred by their teacher, there are no variables associated with any node: each vertex represents a student, and no vertex attributes are taken into account. In the case of organization types, each node has a type, the categories of which are (in this simplified case) non-profit, for-profit, governmental, and intergovernmental. As an example of a network with two variables, consider a graph of ally relationships between nation-states; the first variable captures whether the entity engaged in a military conflict during the previous ten years (a binary variable that takes the value \(True\) or \(False\)), and the second captures total per capita military spending over that same period (an ordinal variable, with each category capturing a range of spending amounts measured in thousands of dollars, such as \([0, 10)\), \([10, 20)\), \([20, 30)\), \(\ge30\)).
To visualize node attributes in a network diagram, the physical aspects of a node’s presentation vary to represent different values; such aspects include color, shape, and size. Sociograms with elements to represent more than two attributes, however, become increasingly challenging to interpret with each additional variable.
Network & Node Measures and Special Graphs
Now that we have covered the foundations of graph elements, we can consider some concepts often implemented in the study social networks. We begin by describing key characteristics that apply to an entire graph, followed by definitions of node-specific measures. We then introduce some special types of graphs.
Graph Characteristics
Distance
There are many important concepts related to the traversal of a graph from one specific node to another. To traverse a graph from one node to another, we follow a path, a sequence of nodes connected by edges, spanning from an origin node to a destination node without repeating any nodes or edges (Wasserman and Faust 1994). For a directed graph, the path follows the direction of each edge. Note that for any pair of nodes in a network, there may exist multiple paths.
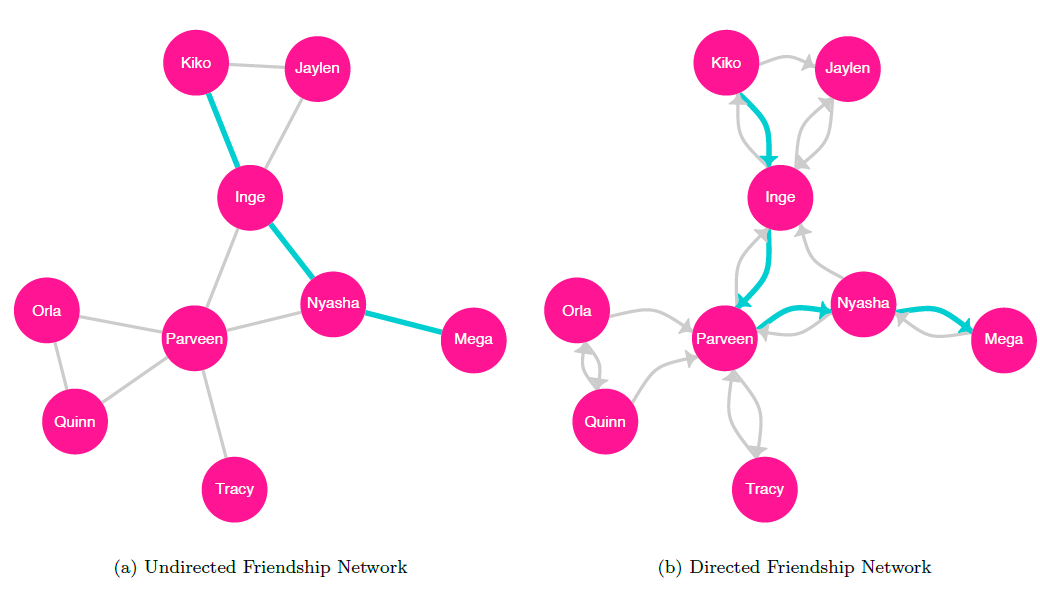
The path length is the number of edges in a given path between two nodes, and the shortest path between two given nodes is called their geodesic (Wasserman and Faust 1994). The sociograms in figure 10.5 highlight the geodesics between Kiko and Mega for both undirected and directed representations of the student friendship network.
The distance between any two nodes, also referred to as the geodesic distance is the length of their geodesic. For example, if nodes \(A\) and \(B\) are connected by an undirected tie, then their geodesic distance is \(1\).
We can find the mean path length, also called the average path length or characteristic path length, by averaging the geodesic distances between all pairs of nodes in the graph (Watts and Strogatz 1998).
The diameter of a network is the maximum geodesic distance between any two vertices in the network (Wasserman and Faust 1994). Note that the path under evaluation is not necessarily the longest path between any two vertices, but the longest of the geodesic paths in the graph.

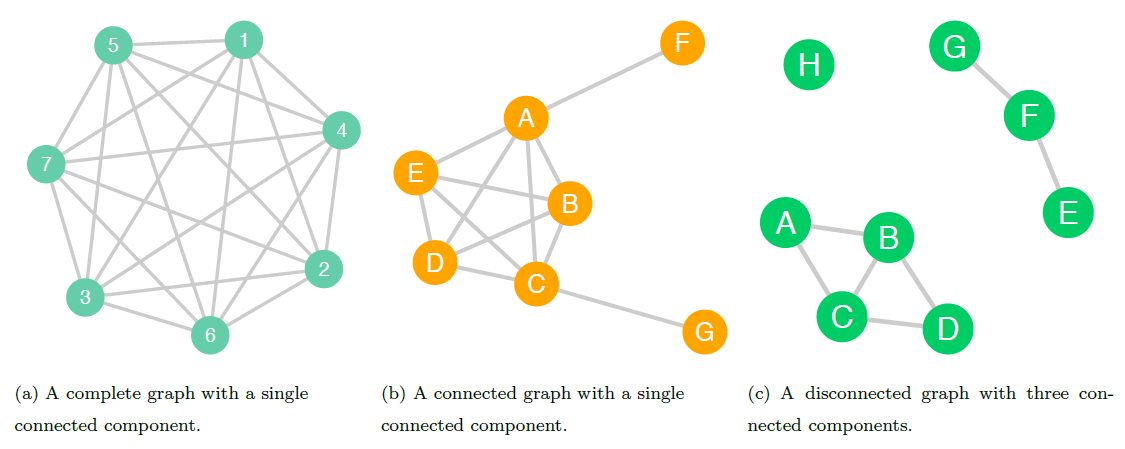
Subgraphs and Components
A network in which each node is directly connected to all the other nodes is called a complete graph (see figure 10.6; this is a special case of a geographic network, which we will describe later.
A graph in which each node can reach all other nodes via a path is called a connected graph (Wasserman and Faust 1994). The graphs shown in figures 10.1, 10.2, 10.3, 10.5, 10.6 are connected graphs. Note that while not every connected graph is a complete graph, all complete graphs are connected graphs.
If we take a subset of the nodes in a graph, including some or all of the edges among the subset of nodes (or, alternately, a subset of edges and all the nodes attached to those edges), the result, called a subgraph, is itself a graph (Wasserman and Faust 1994).
Wasserman and Faust (1994) define three main categories of subgraphs (based on the number of nodes they contain) with special names: isolates, dyads, and triads. An isolate is a single node that is not connected to any other nodes. A dyad is a subgraph of two nodes, either connected or not. A triad is a subgraph of three nodes; in an undirected graph, there may be zero and three edges among the nodes. Note that dyads and triads can include isolates.
If a subgraph is a connected graph—if every node is reachable from every other node—and there are no other nodes connected to the subgraph, then the subgraph is called a connected component. This means that a subgraph consisting of a single node—an isolate—is considered a connected component. Every graph has at least one connected component.
A disconnected graph is one in which at least one node is not reachable via a path from at least one other node (Wasserman and Faust 1994). An equivalent definition describes a disconnected network as one in which at least one connected component is not reachable from another. This means that a disconnected graph has at least two connected components. The network shown in figure 10.6 is a disconnected graph with three connected components.
Node-specific Measures
Centrality
A node’s centrality can be used to gauge how important it is, for various conceptualizations of importance. There are many different measures of centrality; here, we will discuss three such measures: betweenness centrality, closeness centrality, and degree centrality.
Note that though these metrics can be computed for all nodes in a graph, they only make sense for nodes within a connected component; this is because the distance between nodes that are not connected is undefined. These node-specific measures are therefore only computed based on the other nodes in a given node’s connected component Recall, however, that a connected graph contains a single connected component in which each node is connected to all others.
Betweenness centrality. The betweenness centrality metric evaluates a given node’s ability to create connections between other nodes. According to Freeman, who formalized the definition of the metric, betweenness is important because “a vertex falling between two others can facilitate, block, distort, or falsify communication between the two; it can more or less completely control their communication” ((Freeman 1977, 36)). For a given target node, betweenness centrality is found by computing the sum, for all other pairs of nodes in the component, of the ratio of the number of geodesics between the pair of nodes that pass through the target node to the total number of geodesics between the pair of nodes (Freeman 1977). More formally, we can write the definition of betweenness for a node \(v\) as: \[Betweenness(v) = \sum_{i \neq j \neq v}^{n}\frac{g_{ij}(v)}{g_{ij}}\] where \(g_{ij}\) is the number of geodesics between node \(i\) and node \(j\), and \(g_{ij}(v)\) is the number of such paths that pass through node \(v\) (Freeman 1977). The graph below displays each node’s betweenness.

Closeness centrality. Closeness centrality measures how close a node is to others. For a given node in a connected component, closeness centrality is found by computing the reciprocal of the sum of all the distances between the given node and each other node in the component. We can write the definition of closeness for a node \(v\) thus: \[Closeness(v) = \frac{1}{\sum_{i \neq v}^{n}d(v, i)}\] where \(d(v, i)\) is the geodesic distance between nodes \(v\) and \(i\) (Wasserman and Faust 1994). The network in figure 10.7 displays each node’s closeness centrality.
Degree centrality. A third measure of centrality is degree centrality, which considers important nodes to be those that have many neighbors. The degree of a vertex tells us its number of neighbors. To calculate the degree of a vertex in an undirected graph, we can simply count the number of edges it has (Wasserman and Faust 1994). Let us return to the example of an undirected friendship network among classmates as inferred by the teacher (shown in figure 10.8 with each node’s degree labeled); in this network, if Parveen is connected to Inge, Nyasha, Orla, Quinn, and Tracy, then Parveen has a degree of \(5\).
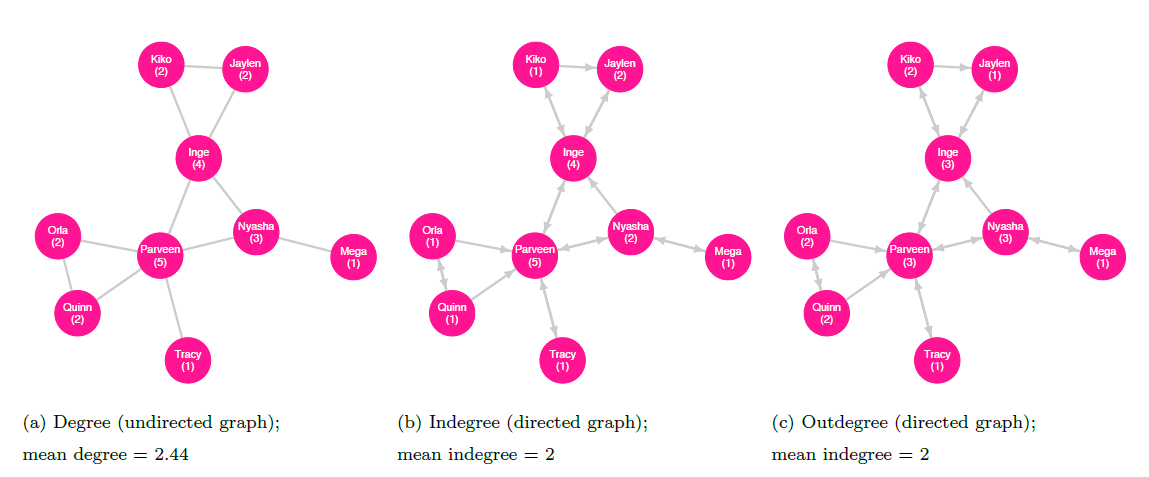
For a directed graph, a node’s indegree is the number of edges terminating there; the outdegree is the number of edges originating from the node (Wasserman and Faust 1994). As an example, we can consider the directed friendship network as described by the students (shown with indegree and outdegree labeled in figures 10.8 and 10.9, respectively). In this network, the students Inge, Nyasha, Orla, Quinn, and Tracy consider Parveen to be a friend, so Parveen has an indegree of \(5\). Parveen, in turn, considers only Inge, Nyasha, and Tracy to be friends and so has an outdegree of \(3\).
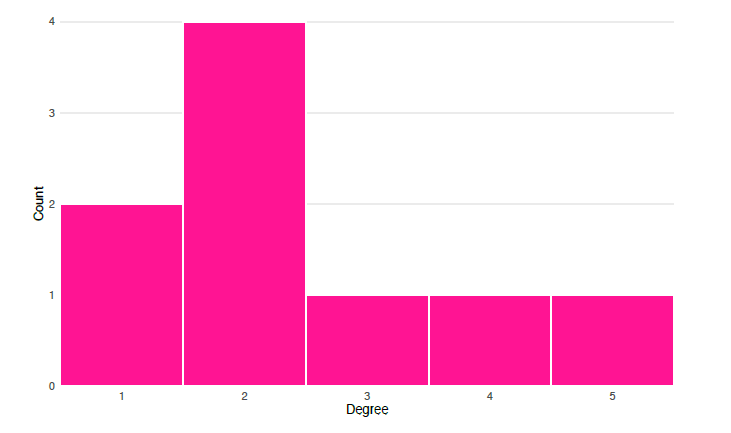
A network’s degree distribution describes the probability of a given node in the graph having a degree of a certain value. In practical terms, we can think of it as a set of numbers, where each reflects the count of nodes in the graph with degree of \(0\), degree of \(1\), degree of \(2\), and so on. The degree distribution for the undirected friendship network is displayed in figure 10.9. The concept of degree distribution will be important later when we discuss power-law networks.
The mean degree of a graph is the mean average of the degrees for all the vertices in the entire graph (Wasserman and Faust 1994). For example, if an undirected network has four nodes with degrees \([1, 1, 2, 2]\), then the mean degree for the network is \(1.5\). If a directed graph has five nodes with indegrees \([0, 1, 3, 3, 3]\), and outdegrees \([1, 2, 2, 2, 3]\), then the mean of the indegrees is \(2\) and the mean of the outdegrees is also \(2\); note that these are equal because every edge extending from some node points to another (Wasserman and Faust 1994).
Clustering
In order to evaluate clustering within a network, we must first introduce the notion of a triple, sometimes called a triplet, which is a connected component with three nodes—that is, it’s a triad with at least two edges. If a triple forms a complete graph—that is, if each node is connected to both the others—then it is a closed triple, also known as a triangle; otherwise, one pair of nodes in the triple are not adjacent so it is an open triple. An ordered triple is one for which the vertex order is a characteristic of the triple; for example, if the vertices \([A, B, C]\) form a triangle, the ordered triples \(ABC\), \(ACB\), \(BAC\), \(BCA\), \(CAB\), and \(CBA\) are each distinct—but note that the triangles formed by each triple are all the same.
For our purposes, we will assume that all edges are undirected when considering triples, triangles, and clustering. Note that in many applications outside the scope of this chapter, this assumption will not hold.
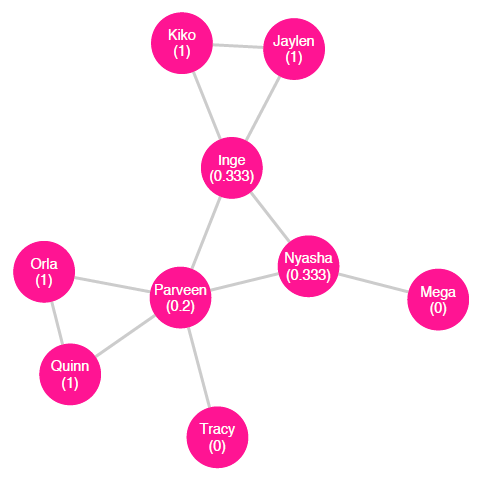
We can now define, for any given node, its local clustering coefficient (also called the local transitivity) by taking the fraction of the pairs of the node’s neighbors that are in turn neighbors with one another—that is, the number of triangles including the node divided by the number of possible triangles (Watts and Strogatz 1998; Opsahl 2013). An equivalent definition given in Saramäki et al. ((Saramäki et al. 2007)) is to compute the ratio of twice the number of triangles that include the given node to the product of the node’s degree and one less than its degree:
\[Transitivity_{local}(v) = \frac{2 \times t_v}{degree(v) \times (degree(v) - 1)}\] where \(t_v\) is the number of triangles that include node \(v\). (Note that for nodes with degree of 1, this results in a zero in the denominator, which means that local transitivity is undefined for such nodes. However, for the purposes of computing the average local clustering coefficient, these undefined values can be replaced with \(0\).) This metric measures cohesion among a given vertex and its neighbors (Barrat et al. 2004). The local transitivity for nodes in the undirected friendship network is shown in figure 10.10 (with undefined values replaced with \(0\)).
We can compute the average local clustering coefficient for a graph \(g\) by taking the mean across all nodes: \[AverageLocalTransitivity(g) = \frac{\sum_{i = 1}^{N}Transitivity_{local}(n_i)}{N}\] where \(n_i\) represents a node identified by its index and \(N\) is the number of nodes in the entire network (Barrat et al. 2004). According to Barrat et al. (2004), this measure “expresses the statistical level of cohesiveness measuring the global density of interconnected vertex triples in the network” (Barrat et al. 2004, 3750).
Finally, to calculate the global clustering coefficient, also called the global transitivity, for a graph \(g\), we take the ratio of thrice the number of triangles to the number of all ordered triples—both closed and open—in the graph: \[Transitivity_{global}(g) = \frac{3 \times Triangles(g)}{Triples_{ordered}(g)}\] where \(Triangles(g)\) is the total number of triangles in graph \(g\) and \(Triples_{ordered}(g)\) is the total number of ordered triples in \(g\) (Opsahl 2013).
Density
The density of a network is the ratio of the number of edges it contains to the number of possible edges. For example, in a network of seven nodes, the number of possible edges is found by the combination \(7C_2 = \frac{7!}{2!(7 - 2)!} = 21\). If there exist \(12\) edges among the nodes, then the density of the network is \(\frac{12}{21} = .57\) or \(57\%\).
Special Graphs
Geographic Networks
A geographic network is one in which each node is connected to the k nearest nodes, with k ranging from \(1\) to the total number of nodes in the network minus \(1\). If k takes on the maximum value—that is, if each node is connected to all the other nodes—then the network is called a complete graph. figure 10.11 shows a geographic network with \(k = 4\).

Random Networks
A random network is one in which, for each pair of nodes, there is a probability \(p\) that there is an edge between them. This probability is a constant for the entire graph and can range from \(0\) to \(1\). The sociogram in figure 10.12 shows a random graph of \(15\) nodes and probability \(p = 0.2\).
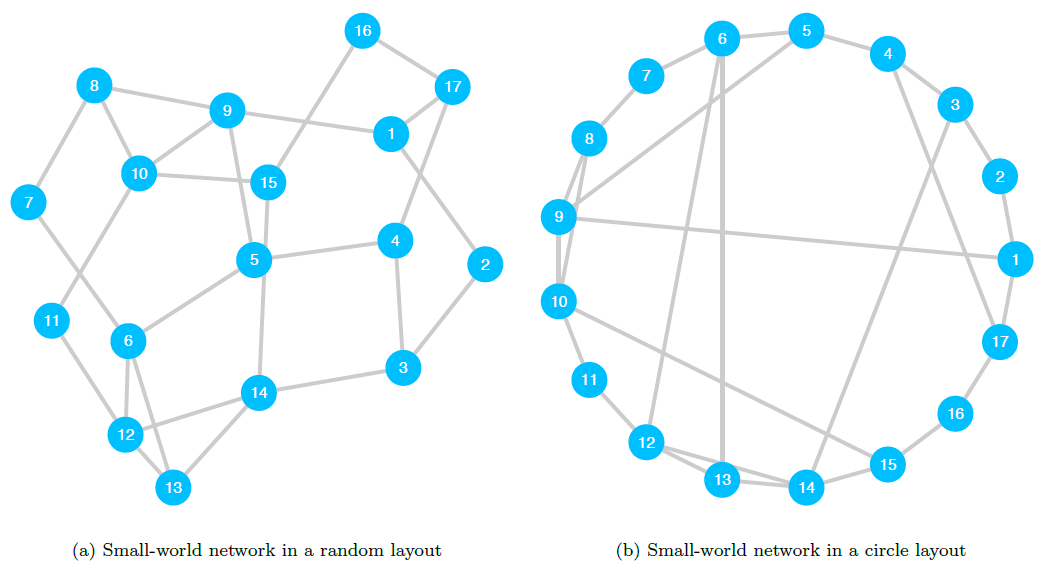
Small-World Networks
The small-world phenomenon describes the idea that in a large population, most people are connected to each other by relatively short chains of acquaintances. In a series of widely known experiments conducted within the United States, Milgram and Travers asked arbitrarily chosen participants to attempt to make contact with a specific target person by mailing or delivering a provided document to someone the participant knew on a first-name basis who was more likely to be personally acquainted with the target person; their findings in one experiment showed that among successful contacts, the average number of intermediaries between the initial participants and the target person was \(5.2\) (Milgram 1967; Milgram and Travers 1969). Dodds, Muhamad, and Watts (2003) conducted an international email study in a similar vein, finding that successful contacts were transmitted across an average chain length of \(4.05\) steps.; when accounting for attrition, they found a median chain length of \(7\) steps.
These experiments show that the small-world hypothesis appears to be consistent with society at large: in just a few degrees of separation, one’s network of friends of friends grows very large.
Small-world networks exhibit two key characteristics: (1) the mean local clustering coefficient is high—that is, on average, a node’s neighbors are highly connected to each other (Watts and Strogatz 1998); and (2) the mean geodesic distance is low—that is, on average, the distance between nodes is short(Watts and Strogatz 1998). Given high average clustering, we might expect such networks to be dense, but in fact, they tend to have relatively few edges (Takes and Kosters 2011). Because they have a small mean path length, the diameter—the largest geodesic distance between any two nodes—is “exponentially smaller than the size of the network” (Kleinberg 2000, 845).
The combination of these features results in a network through which information, preferences, and other conditions (such as infectious disease) can diffuse quickly (Watts and Strogatz 1998).
Figure 10.13 shows two representations of the same small-world network, one with a diameter of \(4\), mean degree centrality of \(3.1\) and a global clustering coefficient of \(0.155\).
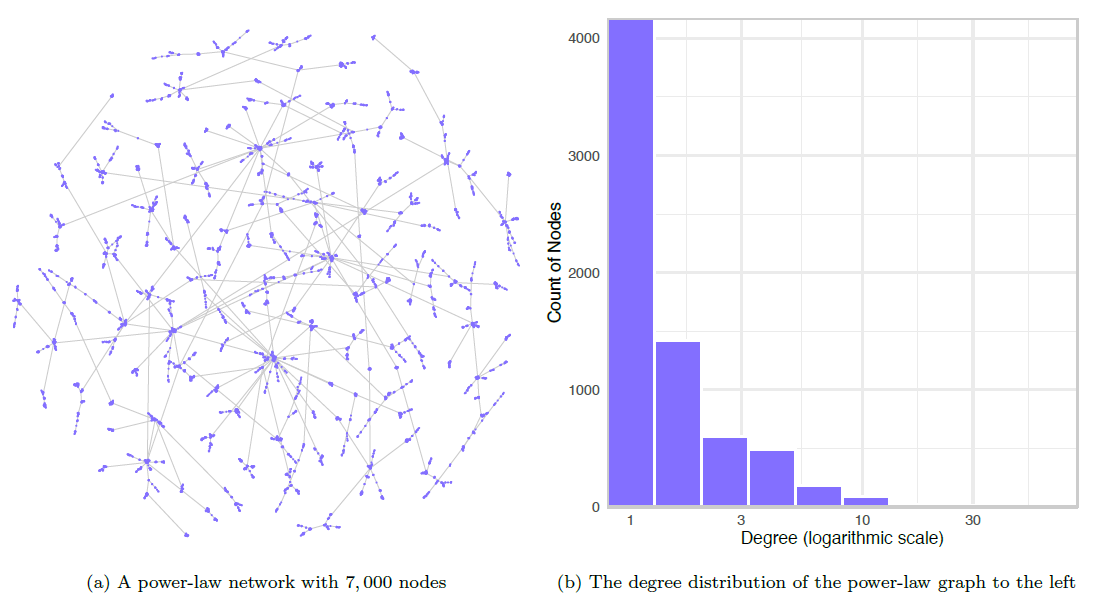
Power-Law Networks
A power-law function is a relationship between two variables, \(x\) and \(y\), of the form \(y = cx ^ a\), where \(a\) and \(c\) are constants. This equation models \(y\) as proportional to \(x ^ a\); as \(x\) changes, \(y\) changes equal to the scale of \(x ^ a\), which is \(c\). The exponent \(a\) can be any real number (though \(a = 0\) yields a horizontal line and \(a = 1\) yields a diagonal line).
Power-law networks are those in which the degree distribution approximates a special case of the power-law function where the scale constant \(c = 1\) (thus why such networks are sometimes called scale-free networks) and the exponent is negative: \(P(x) = x ^ {-a}\). In power-law graphs, the degree distribution shows a large number of low-degree nodes (on the left side of the distribution) and a small number of nodes with very high degree (on the right side of the distribution). As Kadushin notes, for social networks following a power-law distribution, the exponent \(a\) “generally lies between \(2\) and \(3\)” ((Kadushin 2012, 114)).
Scientific studies across a variety of disciplines have indicated that power-law networks abound; Newman, for instance, comments on the “ubiquity of power-law behaviour in the natural world” (Newman 2005). In new research, however, Broido and Clauset challenge the general belief that power-law networks are as widespread as many have claimed, finding specifically that “social networks are at best weakly scale free, and although a power-law distribution can be a statistically plausible model for these networks, it is often not a better model than a non-scale-free distribution” ((Broido and Clauset 2019)).
Applications of Social Network Analysis
Here we describe in detail two studies of social networks in the domain of political science.
Detecting Political Homophily on Twitter
(Colleoni, Rozza, and Arvidsson 2014) analyze the networks of Twitter users in an effort to measure homophily—the extent to which nodes are linked to others with which they share a given characteristic—among Democrats compared to that among Republicans. Their primary research question (p. 317) focuses on the nature of online social news platforms: do these provide their users access to diverse political discourse (the public sphere scenario), or are they more likely to insulate users from others with differing political orientations (the echo chamber scenario)?
The authors implement a machine learning algorithm for an introduction to machine learning methods) to label a set of Twitter users (the egos) by their political leaning based on the content of their politically oriented tweets. Using the same classification method, they identify the egos’ neighbors based on outgoing ties—the users whom the ego follows on Twitter (the alters)—as either Democrats or Republicans (with alters found to be non-political excluded). The result is a directed ego network around each ego, with alters labeled according to their own political leaning.
Next, the researchers calculate each ego’s homophily thus: “the homophily rate is defined as the number of outbound ties directed to alters who share political orientation, divided by the overall number of outbound ties (i.e., directed to alters with similar political orientation plus directed to alters with different political orientation)” (Colleoni, Rozza, and Arvidsson 2014, 324). We can write their equation for homophily as: \[homophily(ego_i) = \frac{alters_{i.s}}{alters_{i.t}}\] where \(alters_{i.s}\) is, for ego \(i\), the number of alters with the same political orientation and \(alters_{i.t}\) is the total number of politically oriented alters. Higher values of homophily (that is, greater than \(0.5\)) mean that a given ego is connected to a greater proportion of alters who share the ego’s political orientation compared to the proportion of alters with the other orientation.
Finally, the authors create two subgraphs: the first is a network of egos and their reciprocal alters (that is, the alters who also follow the ego); this graph represents Twitter as a social platform in which users form reciprocal relationships with other users. The second is a network of egos and their asymmetric ties (that is, the alters who do not follow the ego); this graph represents Twitter as a news platform in which egos follow accounts that disseminate information, while those accounts do not form a relationship with the ego (Colleoni et al. (Colleoni, Rozza, and Arvidsson 2014, 320–21)).
With regard to their main research question—is Twitter a public sphere or echo chamber?—the authors find that the results are contingent on whether Twitter is conceptualized as a social or news platform: “If we look at Twitter as a social medium we see higher levels of homophily and a more echo chamber-like structure of communication. But if we instead focus on Twitter as a news medium, looking at information diffusion regardless of social ties, we see lower levels of homophily and a more public sphere-like scenario” (Colleoni, Rozza, and Arvidsson 2014, 328). This means that the subgraph of reciprocal ties exhibits higher levels of users who are mutually connected to other users sharing their political ideology. The subgraph of asymmetric ties instead exhibits lower levels of homophily, indicating that users are being exposed to diverse political news and opinions.
Measuring the Effect of Centrality on Advocacy Output in a Network of Transnational Human Rights Organizations
(Murdie 2014) explores a network of transnational human rights organizations to assess whether an organization’s position in the network affects their level of political activity. The primary research question is whether an organization’s influence score affects its advocacy output. The author hypothesizes that organizations with high influence scores will engage in more advocacy events.
Murdie constructs a directed network based on inter-organization relationships self-reported by the human rights organizations themselves. She then computes each organization’s influence score, operationalized by a centrality metric called eigenvector centrality. (Briefly, eigenvalue centrality indicates the extent to which a node has many connections to other nodes which themselves have many connections; higher values for eigenvector centrality suggest that a given node wields higher levels of influence over its connections.) The outcome variable is the count of each organization’s advocacy events; one example of an advocacy event is participating in an official meeting with government officials ((Murdie 2014, 18).
Consistent with the author’s hypothesis, the results show that higher centrality scores are associated with greater levels of advocacy. Additionally, the findings indicate that free riders, those organizations that self-report many ties to others but are not in turn reported as connections by other organizations, are associated with somewhat lower levels of advocacy output. Murdie concludes that attempts to foster connections between organizations, particularly between those in the Global South as well as between those in the Global South and the Global North, could yield higher levels of advocacy output and further the organizations’ missions.
Advantages of Social Network Analysis
To discuss the purposes and advantages of social network analysis, we must first describe the different forms it can take. In that vein, Guille et al. (2013) propose a taxonomy of three general categories of social network analysis: identifying “bursty topics”, those that attract “bursts of interest” over a specific range of time; modeling the spread of information, opinions, behavior, or conditions through a network; finding nodes that effectively propagate such information, opinions, or conditions ((Guille et al. 2013, 19, 20, and 24, respectively)). Here, we use the example of the temporally bounded spread of politically oriented misinformation (sometimes called fake news or alternative facts) as a vehicle to explain the advantages of research within each category.
The first category, detecting topics that spike in interest over a given range of time, can be useful for identifying matters of concern to a population. These concerns, of course, could include those based on misinformation, and pinpointing such themes may well be critical to explaining—or even predicting—which topics surge in interest, when, and why. In a similar vein, modeling diffusion through a network—the second category of social network analysis—could inform both inference and forecasting with regard to where and how bursty topics emerge and propagate. In the last category, research focuses on identifying who effectively spreads misinformation, as well as their characteristics and position in the network.
Integrating misinformation research from all three categories could inform efforts to highlight the scope and focus of misinformation, prevent its emergence, or even combat its spread. These goals are especially salient given the proliferation of online bots, which, as Ferrara et al. (2016) describe in their review, can and have been used, either negligently or intentionally maliciously, to diffuse information—and misinformation—about politically oriented topics and in other critical arenas.
The ability to detect topics that spike in interest over a given range of time, combined with models that explain or predict (Ferrara et al. 2016) the diffusion of interest in such topics, could inform the study of fake news. As Ferrara et al. (2016) describe in their review, this is especially salient given that online bots can and have been used, either negligently or intentionally maliciously, to propagate information—and misinformation—about politically oriented topics and in other critical arenas. Scholarship in this area could inform efforts to prevent or combat the spread of such misinformation.
Disadvantages of Social Network Analysis
The benefits notwithstanding, social network analysis is not without its drawbacks. One critical area of concern is with the ethics of research on the widespread relations among a population. Consider, for example, the case of the now-infamous Tastes, Ties, and Time (T3) study (Lewis et al. 2008), which was conducted from 2006 to 2009 (Zimmer 2010).
In this study, T3 researchers accessed the private Facebook profiles of nearly all the students in the 2005 freshman class enrolled in a specific American university (Zimmer 2010), all of whom were members of a Facebook group for their class cohort (Parry 2011). Without the students’ knowledge or informed consent, the team collected data about users’ media preferences (such as music and literature) and friendship ties, once a year for four years, and analyzed changes in the students’ tastes and network ties over time (Zimmer 2010). Researchers then released an ostensibly de-identified version of the dataset as well as its accompanying codebook; these contained individual and aggregate information, respectively. Without even accessing the dataset, Zimmer (2008)—who was unaffiliated with the study—quickly identified the university in question as Harvard College, increasing public concern that individual students in the dataset could also be uniquely identified.
The research project placed its subjects at risk of being publicly identified and, perhaps most critically, linked to their preferences, some or all of which may only have been accessible via the private portion of their Facebook profile. At least one student has been identified and even named (Parry 2011). Such identification could put students at risk of further harm, depending on each student’s individual situation: if, for example, a given student’s preference for queer literature became known to their disapproving family, there could exist the potential for interpersonal tensions, restrictions on financial or other support, or, in an extreme case, bodily harm or even death.
At the very least, the fallout from T3 calls into question data de-identification practices as well as the expectation that any such method could be infallible. Ultimately, the study highlights the need for careful and ethical decision-making when planning, executing, and reporting on social network analyses.
Broader Significance of Social Network Analysis in Political Science
Studies in political science that employ social network analysis methods exist in a variety of forms; here we will consider three classes of studies, each categorized according to the level represented by its network’s nodes. Note, however, that these three classes are by no means exhaustive.
Perhaps most intuitively, nodes in social network analyses may represent individual persons. Some such studies focus on the effects a network may have on its members; Gidengil and Stolle (2009, see, for example,) on the effect of networks and their embedded resources on the political incorporation of immigrant women in Canada. Others consider how individual members influence the nature of the network itself, such as in the aforementioned Colleoni, Rozza, and Arvidsson (2014) Twitter study.
In another class of studies, nodes represent organizations. These may be transnational human rights organizations, as in Murdie’s ((Murdie 2014)) investigation, mentioned in an earlier section. Another is Fowler et al.’s ((Fowler, Grofman, and Masuoka 2007)) evaluation of job placement in a network of university political science departments across the United States.
A third class of inquiry focuses on intergovernmental relations in which nodes represent nation-states. Alcañiz’s ((Alcañiz 2010)) analysis of trans-governmental scientific collaboration among Latin American countries falls into this group.
Conclusion
Social networks exist nearly everywhere that social entities exist. We can analyze these networks to learn about their structure and processes, as well as about the characteristics of their members and the relationships between and among actors. This growing field of inquiry will continue to contribute to political science.
Technological innovations, in particular, have broadened the means by which we generate and manage social network data: in addition to traditional methods, we can now collect or access data with online surveys; from repositories containing datasets automatically produced by computational routines; as well as by combing through administrative, cultural, genealogical, historical, and other records stored in digital archives. Through these avenues, diverse datasets of increasing sizes are becoming more readily available to a larger audience of researchers. Political scientists and other scholars in the social sciences can ask an expanding range of research questions about social networks, and study these networks with an evolving body of methods.
Social network analysis has the potential to refine our interpretations of social relations and processes in the domain of political science. We can use it to confirm or challenge hypotheses; we can sharpen or complicate how we understand actors and relationships. By synthesizing established or contentious knowledge with new insight, we can develop political theory, thought, and practice—as well as advance political and social agendas.
Application Questions
Which of the networks listed in [section 11.2.1] are examples of social networks?
Using the graph in figure 10.15, compute the following:
The betweenness centrality for Akemi and for Dani
The closeness centrality for Brett and for Elvan
The degree centrality for each node
The network’s density
Consider the graph in figure 10.15:
Is this an undirected or directed graph? How can you tell?
Is this a weighted or unweighted graph? How can you tell?
What is the minimum degree for this network? Which node or nodes have this degree?
What is the maximum degree? Which node or nodes have this degree?
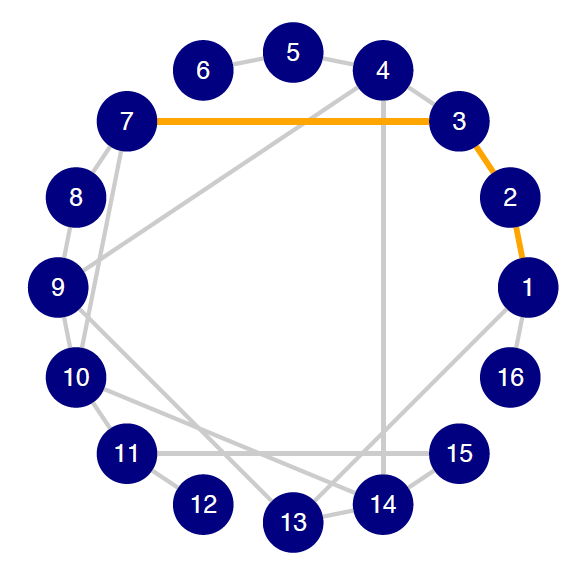
Trace the geodesic between nodes \(1\) and \(7\). What is its length? What is this measure called?
Is the network depicted most likely to be a geographic network, a small-world network, a power-law network, or a random network with \(p = .7\)?
Key Terms
adjacency matrix
betweenness centrality
centrality
closed triple
closeness centrality
complete graph
connected component
connected graph
degree centrality
degree distribution
diameter
directed graph
directed tie
disconnected graph
distance
dyad
edge
geographic network
indegree
isolate
local clustering coefficient
matrix
mean degree
mean path length
neighbors
network
network density
node
open triple
ordered triple
outdegree
path
path length
power-law network
random network
small-world network
social network
social network analysis
subgraph
tie
triad
triangle
triple
triplet
undirected graph
undirected tie
unweighted graph
vertex
weighted graph
Answers to Application Questions
The following are examples of social networks: The genealogical history of the Japanese royal family; email correspondence between workers in a corporation; mentorship and advising among political scientists in academia; and advice-seeking relationships among all current federal circuit judges in the United States
Using the graph in figure 10.5, we find the following:
Betweenness centrality:
Akemi: \(0\)
Dani: \(0.5\)
Closeness centrality:
Brett: \(0.2\)
Elvan: \(0.167\)
Degree centrality:
Akemi: \(1\)
Brett: \(3\)
Chi: \(2\)
Dani: \(2\)
Elvan: \(2\)
Network density: \(0.5\)
Considering the graph in figure 10.15:
This is an undirected network. The edges do not have arrows to indicate asymmetric relationships, so they must be undirected.
This graph is unweighted. There are no weights associated with any of the edges, so it must be unweighted.
The minimum degree is \(1\) and nodes \(6\), \(12\), and \(16\) have a degree of \(1\).
The maximum degree is \(4\) and nodes \(4\), \(9\), \(10\), and \(14\) have a degree of \(4\).
See figure 10.16 for the highlighted path. The geodesic, or shortest path, between nodes \(1\) and \(7\) is \([1, 2, 3, 7]\) and has a path length of \(3\). This metric is called the geodesic distance or simply the distance.
This network is most likely to be a small-world network because it has a large proportion of nodes with average degree centrality, and smaller proportions of nodes with low or high degree centrality. Furthermore: It can’t be a geographic network because degree centrality varies by node. It is not likely to be a power-law network because it has several nodes of the maximum degree (also, it’s unlikely that a graph with only sixteen nodes could follow a power-law distribution). It is not likely to be a random network with \(p = .7\) because that would imply that approximately \(70\%\) of pairs of nodes would be connected, which would, in turn, imply an average degree centrality of \(p \times N = .7 \times 16 = 10.5\); we know, however, that the mean degree is much lower than that as the maximum degree is \(4\).